密码学椭圆曲线加密,ECC椭圆曲线加密算法(一)

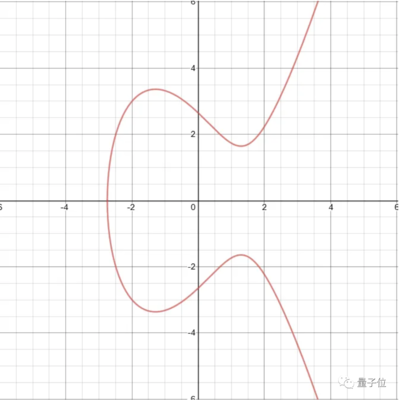
btcaddress:,mWXNJT,VKaHBQs,As,LGVWx,PPHfethaddress:,d,,,,,a,bc,D,,,D,,随着区块链的大热，椭圆曲线算法也成了密码学的热门话题。在Bitcoin生成地址中使用到了椭圆曲线加密算法。椭圆曲线的一般表现形式：椭圆曲线其实不是椭圆形的。得到算法六元组$(p,a,b,G,n,h)在前面提到离散对数问题非常困难，但也不是所有的都困难，有些类型的椭圆曲线就非常脆弱，有非常快速的方法解决，例如$p=hn$时就有多项式时间解决的方法。怎样保证曲线是安全的呢？为了解决这个问题，我们需要再附加一个参数seed$S$。

也就是说，从时间复杂度的角度来看，这个算法是一个的算法。这个方法被称为快速幂算法，原本常用于快速计算某个数的k次幂，这里将其推广到椭圆曲线点乘的快速计算中。为什么要在介绍了椭圆曲线上点的乘法后突然冒出一个快速幂算法？快速幂算法对于椭圆曲线加密有什么意义？因为数学家/密码学家发现。椭圆曲线在密码学中的使用是在,由NealKoblitz和VictorMiller分别独立提出的。椭圆曲线密码学：椭圆曲线密码学（英语：Ellipticcurvecryptography，缩写为ECC），一种建立公开密钥加密的算法，基于椭圆曲线数学。椭圆曲线在密码学中的使用是在,由NealKoblitz和VictorMiller分别独立提出的。

内容加密的秘钥不再需要传递，而是通过运算产生，这样，即使在不安全的网络中进行通信也是安全的。密文的破解依赖于秘钥的破解，但秘钥的破解面临难题，对于RSA算法，这个难题是大数因式分解，对于椭圆曲线算法，这个难题是类离散对数求解。两者在目前都没有多项式时间内的解决办法，也就是说，当位数增多时。椭圆曲线加密(ECC)：高效安全的加密新选择ECC以椭圆曲线方程的魔力催生密钥，的ECC防护力堪比RSA的,，却具备计算量少、速度快的显著优势。在中国，无论是二代身份证还是比特币，都巧妙地采纳了ECC的加密技术。从射影平面的欧几里得几何出发，非欧几何世界中的罗巴切夫斯基几何和黎曼几何。

密码学椭圆曲线加密

要理解ECC椭圆曲线加密算法，就得顺藤摸瓜，一路搞定下面这些原理。于是得到了这样的曲线：这个方程式用来加解密的过程，就不解释了，网上资料不少，密码学的书中也有。其原理基于，射影平面上的加法算法，其正向过程是简单容易的，而加法的逆向过程，则是困难的。我们可以用打台球来比喻。揭示椭圆曲线密码学的神秘面纱NickSulivan，密码学领域的专家，曾在CloudFlare任职并持有硕士学位，他的洞察力在一篇深入浅出的文章中揭示了椭圆曲线密码学（ECC）的精髓。ECC，作为加密技术的强力新秀，被HTTPS安全连接广泛采用，其背后的关键在于其基于数学原理的卓越安全性。不同于RSA。

参加比特币源码研读班后首次写作,看到前辈black写的有关密钥,地址写的很好了,就选了他没有写的椭圆曲线,斗胆写这一篇。在密码学上有两种加密方式,分别是对称密钥加密和非对称密钥加密。对称加密:加密和解密使用的同样的密钥。非对称加密:加密和解密是使用的不同的密钥。椭圆曲线在密码学中的使用是在,由NealKoblitz和VictorMiller分别独立提出的。椭圆曲线密码学：椭圆曲线密码学（英语：Ellipticcurvecryptography，缩写为ECC），一种建立公开密钥加密的算法，基于椭圆曲线数学。椭圆曲线在密码学中的使用是在,由NealKoblitz和VictorMiller分别独立提出的。

椭圆曲线密码体制正是利用这个困难问题设计而来。椭圆曲线应用到密码学上最早是由NealKoblitz和VictorMiller在,分别独立提出的。椭圆曲线密码体制是目前已知的公钥体制中，对每比特所提供加密强度最高的一种体制。解椭圆曲线上的离散对数问题的最好算法是Pollardrho方法，其时间复杂度为。椭圆曲线的这种特性被巧妙地应用到了加密算法中，成为了一种强有力的加密手段。简单来说，ECDLP的困难性构成了椭圆曲线加密算法的核心原理，使得基于此的加密系统具有高度的安全性，成为了现代密码学中不可或缺的一部分。然而，其背后隐藏的数学挑战，使得破解者必须面对一个看似简单实则棘手的难题。

RSA算法RSA是最常见的公钥加密算法之一，它使用一对密钥来进行加密和解密操作。其中一个密钥是公钥，可以公开地用于加密数据，另一个密钥是私钥，用于解密数据。由于公钥和私钥是不同的，因此它不是对称加密算法。椭圆曲线密码学椭圆曲线密码学是一种基于椭圆曲线数学的公钥加密算法。这个方法被称为快速幂算法，原本常用于快速计算某个数的k次幂，这里将其推广到椭圆曲线点乘的快速计算中。为什么要在介绍了椭圆曲线上点的乘法后突然冒出一个快速幂算法？快速幂算法对于椭圆曲线加密有什么意义？因为数学家/密码学家发现，利用快速幂算法计算的时间复杂度是对数级的。

什么是椭圆曲线加密算法

得到算法六元组$(p,a,b,G,n,h)在前面提到离散对数问题非常困难，但也不是所有的都困难，有些类型的椭圆曲线就非常脆弱，有非常快速的方法解决，例如$p=hn$时就有多项式时间解决的方法。怎样保证曲线是安全的呢？为了解决这个问题，我们需要再附加一个参数seed$S$。椭圆曲线在密码学中的使用是在,由NealKoblitz和VictorMiller分别独立提出的。椭圆曲线密码学：椭圆曲线密码学（英语：Ellipticcurvecryptography，缩写为ECC），一种建立公开密钥加密的算法，基于椭圆曲线数学。椭圆曲线在密码学中的使用是在,由NealKoblitz和VictorMiller分别独立提出的。

网上对于椭圆曲线加密过程的介绍过于繁琐，对于只想了解加密如何进行的人来说浪费时间，所以我这里只对关键计算步骤进行介绍，略去椭圆曲线的相关原理（百度一搜一大把）。最最关键且基本只用到的是Ep(a,b)的加法对与椭圆曲线y^,=x^,ax b(modp)：两点P(x,y,Q(x,y,,P≠-Q。尽管离散对数问题在理论上被认为是“hard”的，但并非所有曲线都如此。某些特殊曲线，如[公式]，在Smart

感谢您的来访，获取更多精彩文章请收藏本站。